Die universelle Definition der physikalischen Einheiten

„Von hier bis zum Mond“ kann eine Antwort auf ganz unterschiedliche Fragen sein. Etwa wenn in einem Frage-Antwort-Spiel zwischen dem kleinen und dem großen Hasen die Größe der gegenseitigen Liebe benannt werden möchte. Es kann aber auch die Antwort darauf sein, welche Strecke das Licht während einer einzigen Sekunde zurücklegen kann. Zur Physik, die in der Sphäre des Konkreten, des Dinglichen, des objektiv Messbaren spielt, gehört die zweite Antwort. Denn ihr Forschungsgegenstand ist das Messbare, wobei es durchaus statthaft ist, die Grenzen des Messbaren immer weiter in unbekanntes Land zu verschieben.

Ein Beispiel für eine Erweiterung des Messbereichs ist die Messung des Abstands von der Erde zum Mond: Dazu genügen ein starker Laser und eine gute Stoppuhr. Man peile lediglich mit dem Laser einen der Reflektoren an, die eine Apollo-Mission in den 1960er-/1970er-Jahren auf der Mondoberfläche hinterlassen hat, warte auf ein paar Photonen des reflektierten Lichts und stoppe die Zeit für diesen Weg hin und zurück. Die Stoppuhr wird jetzt etwas mehr als zwei Sekunden anzeigen. Da das Licht die vorteilhafte Eigenschaft hat, immer mit derselben Geschwindigkeit unterwegs zu sein (wenn wir nicht mittendrin das Medium ändern), lässt sich der Abstand Erde-Mond exakt berechnen.

Kinder der französischen Revolution

Solche Abstandsmessungen setzen voraus, dass wir uns einig sind, was unter der Länge Meter zu verstehen ist. Und hier kommt, seit der Meterdefinition aus den 1980er-Jahren, die Lichtgeschwindigkeit ins Spiel. Deren Wert wurde von der Weltgemeinschaft der Metrologie auf einer der alle vier Jahre stattfindenden Generalkonferenzen für Maße und Gewichte (CGPM, Conférence Générale des Poids et Mesures) auf exakt c = 299 792 458 m/s festgelegt. Und „festgelegt“ ist hier der zutreffende Begriff, da die Natur selbst keine mit Einheiten behafteten eindeutigen Zahlenwerte kennt. Diese Zahlenwerte sind menschengemacht und eine Folge dessen, wie wir unser Einheitensystem gebaut haben. Um eine Geschwindigkeit ausdrücken zu können, müssen also zuvor die Zeiteinheit Sekunde und die Längeneinheit Meter vorgegeben sein. Beides nimmt recht willkürlich Bezug auf die Gegebenheiten unseres Planeten: Eine Rotation unserer Erde um die eigene Achse soll, so die Übereinkunft, 24 Stunden dauern, die Stunde 60 Minuten und die Minute 60 Sekunden. Mithin ist die Sekunde der 86 400ste Teil der Tageslänge. Und auch der Meter ist der Erde abgerungen. Ende des 18. Jahrhunderts, im revolutionären Frankreich, sollten mit den Herrschenden auch die „herrschaftlichen Maße“ (Füße, Ellen usw.) abgeschafft werden. Stattdessen war eine Längeneinheit gefragt, der prinzipiell alle Menschen zustimmen konnten. So zogen denn zwei Astronomen los, den Umfang der Erde zu bestimmen. Nach mehreren Jahren geodätischer Vermessung der Strecke Barcelona-Dünkirchen, eines Abschnitts des durch Paris verlaufenden Längengrads, präsentierten die Revolutionäre der Menschheit ein neues, zustimmungsfähiges Längenmaß, nämlich den vierzigmillionsten Teil des Umfangs der (als Kugel gedachten) Erde als die neue Einheit Meter.

Die Meterkonvention

Die Idee, überall auf dem Globus mit einheitlichen Maßen zu messen, geht auf das Jahr 1875 zurück – die Geburtsstunde der Meterkonvention. 150 Jahre später sind über hundert Staaten mittlerweile Mitglieder oder assoziierte Staaten dieses großen Projekts, für eine einheitliche Sprache in der Welt des Messens zu sorgen. Auf den alle vier Jahre stattfindenden Generalkonferenzen für Maße und Gewichte (CGPM, Conferénce Générale des Poids et Mesures) werden die Leitlinien hierzu festgelegt und, falls nötig, grundlegende Änderungen im Einheitensystem verabschiedet. So zu erleben in Versailles im November 2018, als die Delegierten aller Staaten einmütig mit „Ja“ auf die Frage antworteten, ob in Zukunft Naturkonstanten die Einheiten definieren sollen.

Der daraus resultierende Ur-Meter, als in einen Platin-Iridium-Stab gegossene Längeneinheit, trat dann seinen Siegeszug um die Welt an. Im Jahr 1875 verabredeten die ersten 17 Staaten (darunter das damalige Deutsche Reich), von nun an mit denselben Maßen zu messen. Sie unterzeichneten, quasi als Pioniere, die sogenannte Meterkonvention, die zunächst die Einrichtung und die Finanzierung des Büros für Maße und Gewichte in Paris regelte. Bis 2024 sind 64 Staaten der Meterkonvention beigetreten, weitere 37 sind assoziiert.

Problematische Verkörperungen

So schön und wertvoll und anschaulich ein verkörpertes Maß wie der Ur-Meter auch ist, hat er, bei genauem Hinsehen, doch eine Reihe von Problemen. Schon die Temperatur verändert seine Länge; die Gravitation zerrt, je nachdem, wie er festgehalten wird, an seiner Form; die Verwendung im Labor hinterlässt Gebrauchsspuren. Schließlich: Nur ein Objekt allein, auf das sich alles bezieht, genügt nicht. Es müssen möglichst identische Kopien hergestellt und verteilt werden. Und: Längenmaßstäbe werden nicht nur in der Größenordnung Meter gebraucht, sondern überall auf der Längenskala zwischen Mikro- und Makrokosmos. Ein Nano- oder Femtometer lässt sich ebenso wenig mit einem Ur-Meter ausmessen wie ein Kilometer oder gar astronomische Distanzen.

Überwinden lassen sich diese Probleme nur, wenn man die Verkörperung des Maßes aufgibt und an dessen Stelle etwas tritt, das per se unveränderlich und auf der ganzen Skala der Einheit gültig ist: Naturkonstanten, also unveränderliche Merkmale der Natur.

So wurde bereits im Jahr 1967 die sehr irdisch geprägte Sekundendefinition durch die Zeitmessung über Atomuhren ersetzt. Die Sekunde bezieht sich seitdem auf eine definierte Zahl von Schwingungen in der Elektronenhülle des Cäsium­atoms, den sogenannten Uhrenübergang. Eine der CGPM-Konferenzen für Maße und Gewichte legte die Frequenz dieses Uhrenübergangs auf ∆ν = 9 192 631 770 s⁻¹ fest. Der reine Zahlenwert selbst ist, ebenso wie bei der Lichtgeschwindigkeit, nicht naturgegeben, sondern spiegelt vielmehr die historische Definition der jeweiligen Einheit wider.

Während also die Sekunde und der Meter schon seit den 1960er- und 1980er-Jahren diesen erstrebenswerten Zustand der Anbindung an Naturkonstanten erreicht hatten, erforderte es die gesamte Messkunst der Metrologie, um auch die anderen (Basis-)Einheiten auf solch fundamentale Füße zu stellen. Welche Naturkonstanten dafür infrage kamen, lag teilweise auf der Hand: Für die elektrische Stromstärke als bewegte Ladung pro Zeit, gemessen in Ampere, gab es die Elementarladung e; für die thermodynamische Temperatur, gemessen in Kelvin, bot sich die Boltzmann-Konstante k_B an; und für die Stoffmenge, gemessen in Mol, die Avogadro-Konstante N_A. Beim Kilogramm, der Einheit der Masse, gab es jedoch längere Diskussionen in der metrologischen Gemeinschaft. Während manche Expert:innen eine masseartige Naturkonstante, etwa die Masse des Elektrons, bevorzugten, argumentierten andere für die Planck-Konstante h, die schon bei allen Realisierungen der elektrischen Größen eine entscheidende Rolle gespielt hatte.

Für eine neue Kilogrammdefinition einigten sich die Wissenschaftler:innen schließlich auf die Planck-Konstante. Diese musste nun so gut wie nur irgend möglich gemessen werden, um einen möglichst nahtlosen Übergang von der alten zur neuen Masseeinheit zu schaffen. Ein neues, auf der Basis von h definiertes Kilogramm sollte also die Masse des alten Ur-Kilogramms möglichst exakt reproduzieren. Zwei prinzipiell unterschiedliche Experimente sollten dem Kilogramm ein zukünftig stabiles Dasein verschaffen: Bei der Wattwaage kompensiert eine elektromagnetische Kraft die Schwerkraft, die auf ein Massestück wirkt. Hierbei werden mehrere elektrische Quanteneffekte ausgenutzt, was dazu führt, dass dieses Experiment direkt einen Wert der Planck-Konstante h mitliefert. Die Protagonist:innen dieses Experiments arbeiteten in Kanada, in den USA und in England. Das dazu alternative und von der Physikalisch-Technischen Bundesanstalt favorisierte Avogadro-Experiment konnte in einem nahezu perfekten Einkristall, einer Siliziumkugel, die Zahl der Atome bestimmen und auch daraus den Wert der Planck-Konstante h ableiten. Die Ergebnisse aus beiden Experimenten waren untereinander konsistent – und damit der Weg zu einem neuen Kilogramm offen.

Genau Ein Kilogramm Atome

Am meisten Sorgen im alten Einheitensystem bereitete das Kilogramm, das in einem wörtlichen Sinne in die Jahre gekommen war: Es beruhte auf der Masse eines Metallzylinders aus dem 19. Jahrhundert, der in einem Tresor im Internationalen Büro für Maß und Gewicht (BIPM) in der Nähe von Paris lag. Jedes Kilogrammstück auf der Welt bezog sich auf dieses Ur-Kilogramm. Und nicht nur das: Viele andere Einheiten, wie das Mol (für die Stoffmenge) oder das Ampere (für die Stromstärke), waren von ihm abhängig. Hatte das Kilogramm ein Problem, hatten es die anderen Einheiten automatisch auch. Und das Kilogramm hatte „Gewichtsprobleme“, was sich bei den Vergleichen mit den vielen nationalen Kopien zeigte. Seine Masse veränderte sich in der Größenordnung von Mikrogramm pro Jahr – metrologisch eine Katastrophe!

Ein Lösungsweg bot das Avogadro-Experiment. Die Idee: Man nehme Atome eines ausgewählten Isotops (Silizium-28), züchte einen perfekten Einkristall und forme daraus eine nahezu ideale Kugel. Anschließend nehme man alle nötigen Messungen vor, um die Abweichungen von diesen idealen Bedingungen festzustellen. Nach vielen forschungsintensiven Jahren und technologischen Fortschritten konnte die Zahl der Atome in einem solchen Einkristall aus Silizium-28 mit einer Genauigkeit von etwa 10⁻⁸ bestimmt werden. Gleich zwei der gesuchten Naturkonstanten waren das Ergebnis: die Avogadro-Konstante für die Definition der Einheit Mol (N_A = 6,022 140 76 × 10²³ mol⁻¹), sowie die Planck-Konstante für die des Kilogramms. Letztere wurde nach Abgleich mit den Wattwaagen-Ergebnissen festgelegt auf h = 6,626 070 15 × 10^–34 J s.

Das Einheitensystem als universelle Sprache

Die meisten Menschen werden in ihrem Alltag nichts von der Revolution im Internationalen Einheitensystem (SI, Système International d‘unités) bemerkt haben. Wäre es anders, hätte die metrologische Forschung auch schlecht gearbeitet. Für die Wissenschaft sind die Neudefinitionen ein enormer Fortschritt, da das Einheitensystem nunmehr eine universelle Sprache darstellt, die sich prinzipiell zu jeder Zeit und an jedem Ort im gesamten Universum verstehen lässt. Diese Idee, die Max Planck schon um 1900 mit seinen „natürlichen Einheiten“ hatte, konnte über ein Jahrhundert später praktische Realität werden. Und das neue SI besitzt nun eine sehr stringente innere Logik. So entfällt im neuen SI die Unterscheidung zwischen Basiseinheiten und abgeleiteten Einheiten. Vielmehr sind alle Einheiten jetzt aus Naturkonstanten „abgeleitet“ und in diesem Sinne gleichwertig.

Während sich in der Wissenschaft die Neudefinitionen sofort auswirken, wird die Technik eher eine positive Langzeitwirkung spüren. Denn ein Clou am neuen Einheitensystem ist, dass in ihm keinerlei technische Barrieren mehr eingebaut sind. Schwankte etwa im alten System die Masse des Ur-Kilogramms in einer gewissen Größenordnung, so war die beste erreichbare Genauigkeit einer Wägung eben durch diese Schwankungsbreite begrenzt. Im neuen SI dagegen gibt es keine Schwankungen mehr, da die Naturkonstanten verbindlich festgelegte Werte bekommen haben. So ist die Kilogramm-Definition jetzt unabhängig von möglichen Veränderungen von Vergleichskörpern. Alle elektrischen Einheiten inklusive des Ampere sind als Quantenrealisierungen (über den Josephson- und den Quanten-Hall-Effekt oder durch Zählen von Elektronen pro Zeit) Teil des Systems. Und nicht zuletzt ist das Mol nun auch definitorisch über eine festgelegte Anzahl von Teilchen (die Avogadro-Konstante) einer spezifizierten Substanz erfasst. Daher gilt im neuen SI: Kann genauer gemessen werden, können auch die Einheiten genauer realisiert werden – ohne erneute Änderung der zu­grunde­liegenden Definition. In einer hochtechnischen Welt, in der weder die Längenteilungen beim Nanometer aufhören werden noch die Zeitteilungen bei Femtosekunden, ist diese technische Offenheit des neuen Einheitensystems gegenüber allen zukünftigen Genauigkeitsfortschritten ein großer Gewinn. Und diese Offenheit gilt auf der gesamten Skala der jeweiligen Einheit, da die Naturkonstanten keinen speziellen Skalenabschnitt hervorheben.

Das auf Naturkonstanten basierende Einheitensystem ist ein Meilenstein der Wissenschafts- und Kulturgeschichte. Die technologischen Früchte, die daraus erwachsen, werden wir in den kommenden Jahren und Jahrzehnten ernten. Die Fragen des kleinen und des großen Hasen bleiben davon natürlich unberührt.

Der Quanten-Hall-Effekt

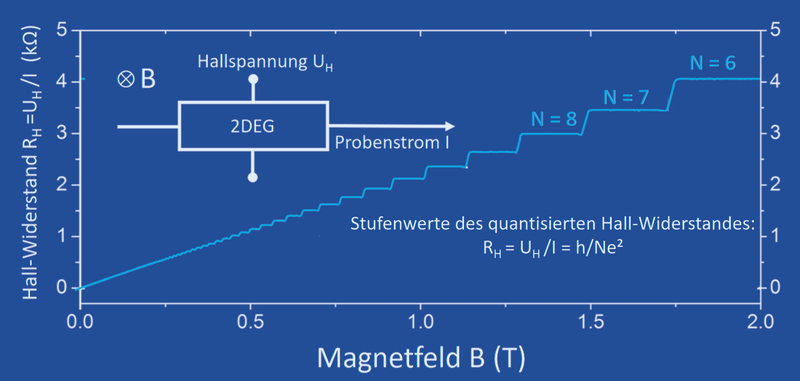
Edwin Hall beobachtete 1879, dass bei einem elektrischen Leiter im Magnetfeld eine Spannung auftritt, die proportional mit der Stärke des Stromes und des Magnetfelds ansteigt. Mit diesem Hall-Effekt lässt sich beispielsweise die Konzentration von elektrischen Ladungsträgern bestimmen. Das ist besonders bei Halbleitern wichtig, bei denen die Ladungsträgerkonzentration und somit die Funktionsweise von Bauelementen durch Dotierstoffe verändert werden kann.

Grundlagenforschung an dem wichtigsten Bauelement der Mikroelektronik, dem Silizium-Feldeffektransistor, führte 1980 zur Entdeckung des Quanten-Hall-Effekts. Anders als beim klassischen Hall-Effekt steigt hier die Hall-Spannung mit der Stärke des Magnetfeldes nicht geradlinig an, sondern zeigt Stufen. Der Widerstand dieser Stufen (die gemessene Hall-Spannung geteilt durch den Probenstrom) hängt neben der Quantenzahl N nur von den Fundamentalkonstanten h (Planck-Konstante) und e (Elementarladung) ab. Voraussetzung für die Beobachtung dieses Quantenphänomens ist das Zusammenspiel von zwei Quanteneffekten. Dafür muss der elektrische Leiter so dünn sein, dass sich die Elektronen nur in einer Ebene frei bewegen können. Das ist bei Feldeffekttransistoren, bei denen der Stromfluss in einer dünnen Oberflächenschicht geschieht, erfüllt. Zusätzlich muss senkrecht zu diesem Elektronensystem ein so starkes Magnetfeld angelegt werden, dass die Elektronen geschlossene Kreisbahnen durchlaufen. Durch diese zwei Quanteneffekte wird die ursprünglich freie Bewegung von Elektronen unterbunden und nur noch ganz bestimmte Elektronenenergien sind erlaubt, was zu den Quantensprüngen im Hall-Widerstand führt. Die quantisierten Widerstandswerte werden weder durch Verunreinigungen im Festkörper noch durch die für die Messung notwendigen elektrischen Kontakte beeinflusst, sodass sich der quantisierte Hall-Widerstand überall in der Welt mit einer Genauigkeit von mindestens zehn Ziffern reproduzieren lässt.

Da die Werte für e und h im internationalen Einheitensystem exakt definiert sind, hat auch die Von-Klitzing-Konstante h/e² einen international festgelegten Wert. Der Quanten-Hall-Effekt lässt sich also überall im Universum zur Eichung elektrischer Widerstände nutzen.

Klaus von Klitzing

Immer die gleiche Spannung?

Ein Volt ist ein Volt ist ein Volt? In der Theorie vielleicht, aber in der Praxis ist die Einheit der Spannung stark davon abhängig, mit welchen technischen Mitteln man sie realisiert. Sehr genau lässt sich das Volt mithilfe eines Quanteneffekts bestimmen, den Brian D. Josephson 1962 entdeckte. Die nach ihm benannten Jo­seph­son-Spannungsnormale gehören zusammen mit Quanten-Hall-Widerstandsnormalen zu den „Goldstandards“ der elektrischen Quantenmetrologie, also demjenigen Bereich der modernen Messtechnik, der Vergleichswerte und Messapparaturen auf universell gültige Quantenphänomene abstützt.

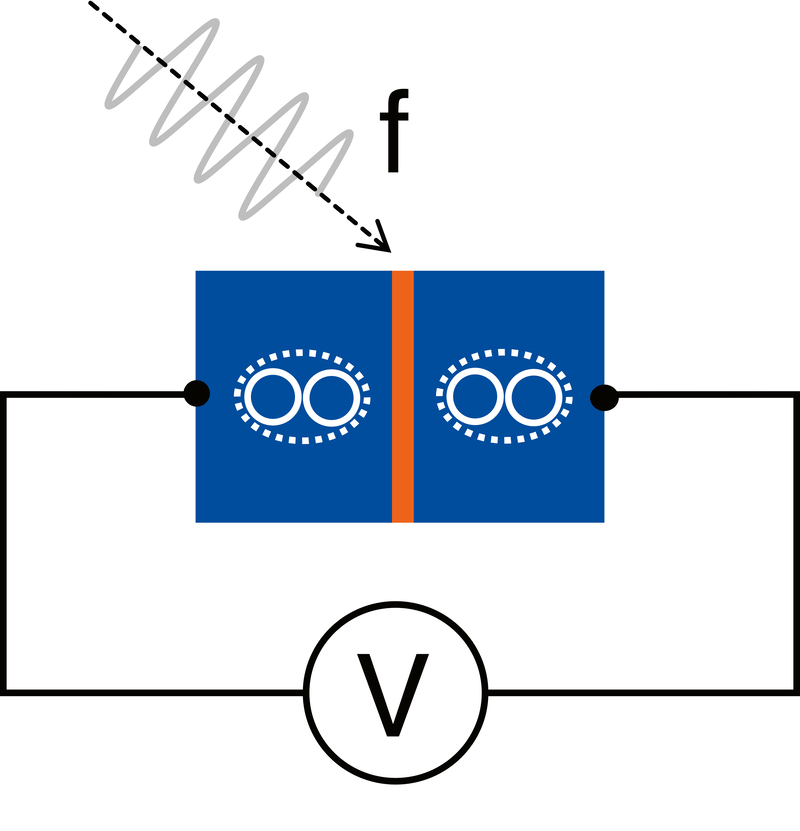
Josephson-Spannungsnormale basieren auf elektrischen Schaltungen, die aus Josephson-Kontakten aufgebaut sind. Ein Josephson-Kontakt wiederum besteht aus zwei supraleitenden metallischen Elektroden, die durch eine sehr dünne normalleitende (also nicht supraleitende) oder isolierende Barriere getrennt sind. Der Übergang von Ladungsträgern zwischen den beiden Elektroden ist damit durch quantenmechanisches „Tunneln“ von Cooper-Paaren (Elektronenpaare in Supraleitern) möglich. Bestrahlt man diesen Kontakt mit einer Mikrowelle, so treten zwischen den Elektroden konstante und genau definierte elektrische Spannungen auf (Josephson-Effekt). Diese quantisierten Spannungswerte sind proportional zur Frequenz der eingestrahlten Mikrowellenfrequenz sowie zum Quotienten aus der Planck-Konstante h und der Elementarladung e.

Da die Werte für e und h im internationalen Einheitensystem exakt definiert sind und die Mikrowellenfrequenz sich mit sehr hoher Genauigkeit bestimmen lässt, können Josephson-Kontakte als ideale Frequenz-zu-Spannungs-Wandler genutzt werden. Seit 1990 sind sie die weltweit verbindliche Grundlage für die Reproduktion und Realisierung der elektrischen Spannungseinheit „Volt“ mit höchster Genauigkeit und Präzision.

In der Praxis genutzte Mikrowellenfrequenzen liegen im Bereich einiger zehn Gigahertz, weshalb ein einzelner Josephson-Kontakt eine elektrische Spannung unterhalb eines Millivolts erzeugt. Zur Darstellung von Spannungen von einem Volt oder mehr benötigt man Serienschaltungen aus mehreren Tausenden bis zu Hunderttausenden Josephson-Kontakten. Durch Fortschritte bei der Herstellung hochintegrierter Serienschaltungen aus Josephson-Kontakten lassen sich Josephson-Spannungsnormale vor allem für die immer stärker zunehmenden Wechselstromanwendungen nutzen.

Hansjörg Scherer